概率论与十连保底

参考文章：10 连抽保底的概率模型

在线演示：CodeSandBox

前不久看到了一篇很有意思的文章，是云风大大写的介绍十连抽的保底概率模型。经常玩抽卡二游的小伙伴应该都知道十连保底的机制，对于我这种脸黑的非酋玩家简直就是救命神器，如果没有保底，是真可能非到怀疑人生的。而从开发者的角度来看，我其实也思考过十连保底的实现方式，但是直到看完这篇文章，才明白自己想简单了。

模拟抽卡

首先，我们先构建一个简易的抽卡模拟器：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37


let total = 0 // 抽卡总数
let out = 0 // 抽出的数量
let distribution = [] // 出货分布

const test = (times) => {
  let counter = 0; // 记录出货抽数
  // 抽 n 次
  for (let i = 0; i < times; i++) {
    counter++
    total++
    if (某种出货条件) {
      distribution[counter] = (distribution[counter] || 0) + 1
      counter = 0
      out++;
    }
  }
  print()
}

const print = () => {
  const formatRate = (num) => (num * 100).toFixed(2) + "%";
  
  console.log(distribution)

  const result = {
    "抽卡总次数": total,
    "出货量": out,
    "理论出货率": formatRate(RATE),
    "实际出货率": formatRate(out/total),
  }

  console.log(
    Object.entries(result).map(([key,value]) => `${key}：${value}`).join("；")
  )
}

test(1000000)

通过这种方式，我们可以自定义某种出货条件，通过重复多次的模拟抽卡，记录数据分布。

无保底的情况

我们首先看没有任何约束条件的无保底的抽卡方式，给定一个概率阈值 RATE，为了方便起见我们引入 echarts 库来可视化概率分布：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66


+ import * as echarts from 'echarts';

+ const chartDom = document.getElementById('chart');
+ const myChart = echarts.init(chartDom);

+ const RATE = 0.1

const test = (times) => {
  let counter = 0; // 记录出货抽数
  // 抽 n 次
  for (let i = 0; i < times; i++) {
    counter++
    total++
-   if (某种出货条件) {
+   if (Math.random() < RATE) {
      distribution[counter] = (distribution[counter] || 0) + 1
      counter = 0
      out++;
    }
  }
  print()
}

const print = () => {
  const formatRate = (num) => (num * 100).toFixed(2) + "%";

- console.log(distribution)

  const result = {
    "抽卡总次数": total,
    "出货量": out,
    "理论出货率": formatRate(RATE),
    "实际出货率": formatRate(out/total),
  }

+ const x = []
+ const y = []

+ distribution.forEach((count, index) => {
+   if (index === 0) return
+   x.push(index)
+   y.push(count || 0)
+ })

+ const option = {
+   xAxis: {
+     type: 'category',
+     data: x
+   },
+   yAxis: {
+     type: 'value'
+   },
+   series: [
+     {
+       data: y,
+       type: 'bar'
+     }
+   ]
+ };

+ myChart.setOption(option);
  console.log(
    Object.entries(result).map(([key,value]) => `${key}：${value}`).join("；")
  )
}

抽卡一百万次的结果如下：

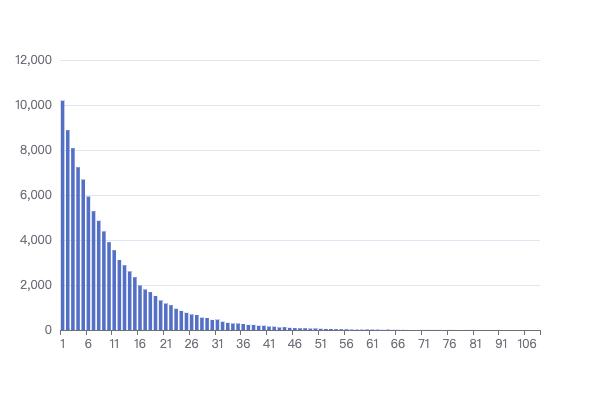
抽卡总次数：1000000；出货量：100525；理论出货率：10.00%；实际出货率：10.05%

可以看出，整体的分布是一个几何分布，它所表示的是第 x 抽才出货的概率分布。以 10% 出货率为例，此时的概率密度函数为： $$ f(x)=p(1-p)^{x-1},\quad p=0.1 $$ 接下来，我们来手动改变一下它的概率分布

最简单的实现——直接保底

直接保底是最简单的一种实现，可能大家的第一反应都是这种方式，即记录抽卡次数，如果上一次出货距离这一次的抽数达到了保底抽数，那么这一抽就不需要再判定概率，直接给予出货，体现在代码上如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23


const RATE = 0.1
+ const GUARANTEE = 10

let total = 0 // 抽卡总数
let out = 0 // 抽出的数量
let distribution = [] // 出货分布


const test = (times) => {
  let counter = 0; // 记录出货抽数
  // 抽 n 次
  for (let i = 0; i < times; i++) {
    counter++
    total++
-   if (Math.random() < RATE) {
+   if (counter === GUARANTEE || Math.random() < RATE) {
      distribution[counter] = (distribution[counter] || 0) + 1
      counter = 0
      out++;
    }
  }
  print()
}

输出的结果如下：

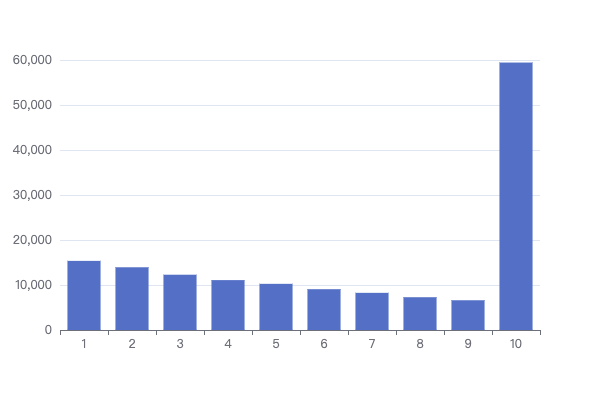
抽卡总次数：1000000；出货量：153576；理论出货率：10.00%；实际出货率：15.36%

可以看出，第十抽才出的概率飙升，占到了将近 40%。这种算法确实是实现了十连的保底，但是和我们理想中的保底还是有所差距，为什么？从图表中我们可以看出，概率分布太不自然了，如果十个人来抽卡，其中有四个人会吃到 10 抽的保底，更好的解决方案是把 10 抽之后的概率平摊到 1-10 抽的这个区间中，而非简单的全部 squash 到第十抽上。

这里隐含着一个看似无法实现的要求，即要让后面的出货概率影响到前面的出货概率，可能听起来有点奇怪，但其实解决思路很简单——我们不在每次抽卡时做判断，而是在每次出货后就确定下一抽应该是第几抽出，这样就不用考虑后面的概率了，要实现这一点，我们每次只需要在 1-10 这十个数里面抽一个数就可以了，具体怎么抽，则会在下文详细阐述

尝试改造

当我们把目光从出货的抽数转向两次出货之间的抽数时，我们实际上分析的就不再是事件发生的概率了，而是事件发生的频率。面对事件发生的频率，我们需要分析的是另一种分布——指数分布

如何简单地理解指数分布，实际上只需要理解一句话，以抽卡事件为例，两次出货中间间隔抽数为 x 的概率，等同于连续 x 抽不出货的概率。后者是一个泊松分布

指数分布的概率密度函数如下： $$ f(x)=\lambda e^{-\lambda x},\quad x \gt 0 $$ 其中 $\lambda$ 表示的是事件发生的平均速率，在上述场景下平均每 10 抽会有一次出货，取单位时间为一抽， $\lambda$ 为 0.1

我们首先要做的是改变随机数的生成方式，从原先的平均分布改为指数分布，这里我们会用到一种方法叫逆变换采样，它能将 (0,1] 上均匀分布的样本映射到指数分布，我们只需要知道公式就行了。顺着这个思路，我们继续改造抽卡函数：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30


const RATE = 0.1
const TIMES = 1000000
+ const EXPECTION = Math.trunc(1 / RATE)

+  const genTarget = () => {
+   let p = Math.floor(Math.log(1 - Math.random()) * (-EXPECTION))
+   // 核心公式，取 1-x 是为了防止出现 ln0 的情况
+   while (p > 10 || p <= 0) {
+     p = Math.floor(Math.log(1 - Math.random()) * (-EXPECTION))
+   }
+   return p
+ }

const test = (times) => {
  let counter = 0; // 记录出货抽数
+ let target = genTarget()
  // 抽 n 次
  for (let i = 0; i < times; i++) {
    counter++
    total++
-   if (counter === GUARANTEE || Math.random() < RATE) {
+   if (counter === target) {
      distribution[counter] = (distribution[counter] || 0) + 1
      counter = 0
      out++;
+     target = genTarget()
    }
  }
  print()
}

结果如下：

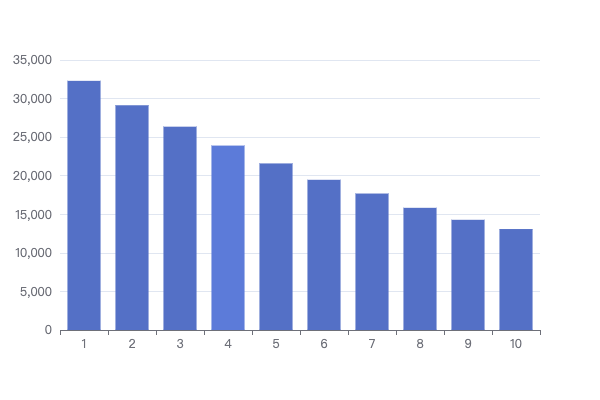
抽卡总次数：1000000；出货量：213653；理论出货率：10.00%；实际出货率：21.37%

可以看出，完美地实现了我们的需求，既融合了保底机制，又保持了概率分布是标准的指数分布。

所以，其实你的每一发单抽，早就在上一次出货时就已经注定了结局hh