Featured image of post 优先队列和寻找中位数
前端

优先队列和寻找中位数

使用 TypeScript 实现

前言

LeetCode 上有一道很经典的算法题，数据流中的中位数，题目描述很简单，就是让你得到中位数，比如 [1, 2, 3] 的中位数就是 3，[1, 2, 3, 4] 的中位数就是 (2 + 3) / 2 = 2.5，解法也有很多，比如最简单的，直接维护一个有序数组，每次插入数据时就让对应位置后方的数据全部后移一位然后插入。

但是这样的方法显然十分低效，我们只关心中位数，而其他部分实际上根本不需要保持有序。观察题目要求，假设使用数组数据结构，中位数实际上是把数组分成了等长的两部分，左边的部分都小于它，右边的部分都大于它（偶数个时的中位数是通过计算得到的）。那么问题就十分明了了，我们如果可以维护两个数组，其中一个只维护最大值，另一个只维护最小值，不就可以很轻松地得到中位数了吗。

这种数据结构就是 堆(Heap)

正文

堆

堆是一颗 完全二叉树，且节点的值一定不大于（或不小于）其子节点的值。

如果节点的值都大于其子节点，则成为 大顶堆/大根堆(max-heap)

反之就是 小顶堆/小根堆(min-heap)

如下图就是一个小根堆：

小根堆

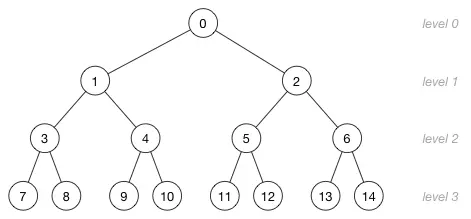
由于堆是一个完全二叉树，所以我们完全可以使用数组来存储，而且节点满足以下规律：

若当前节点下标为 x，则有

  1. 当前节点的左节点下标为 2x+1
  2. 当前节点的右节点下标为 2x+2

利用堆的这些性质，再给它加上插入和删除等方法，我们就得到了一个新的数据结构：优先队列

优先队列

插入（push）

优先队列的插入大致分为如下几个流程：

  1. 把节点插入到堆的最后
  2. 将插入节点与父节点作比较，判断是否满足大小关系
  3. 如果不满足则交换父节点和插入节点，然后继续重复比较，直到满足大小关系

这样的一个流程被称为 上浮(shiftUp)，小根堆的插入流程大致如下图所示：

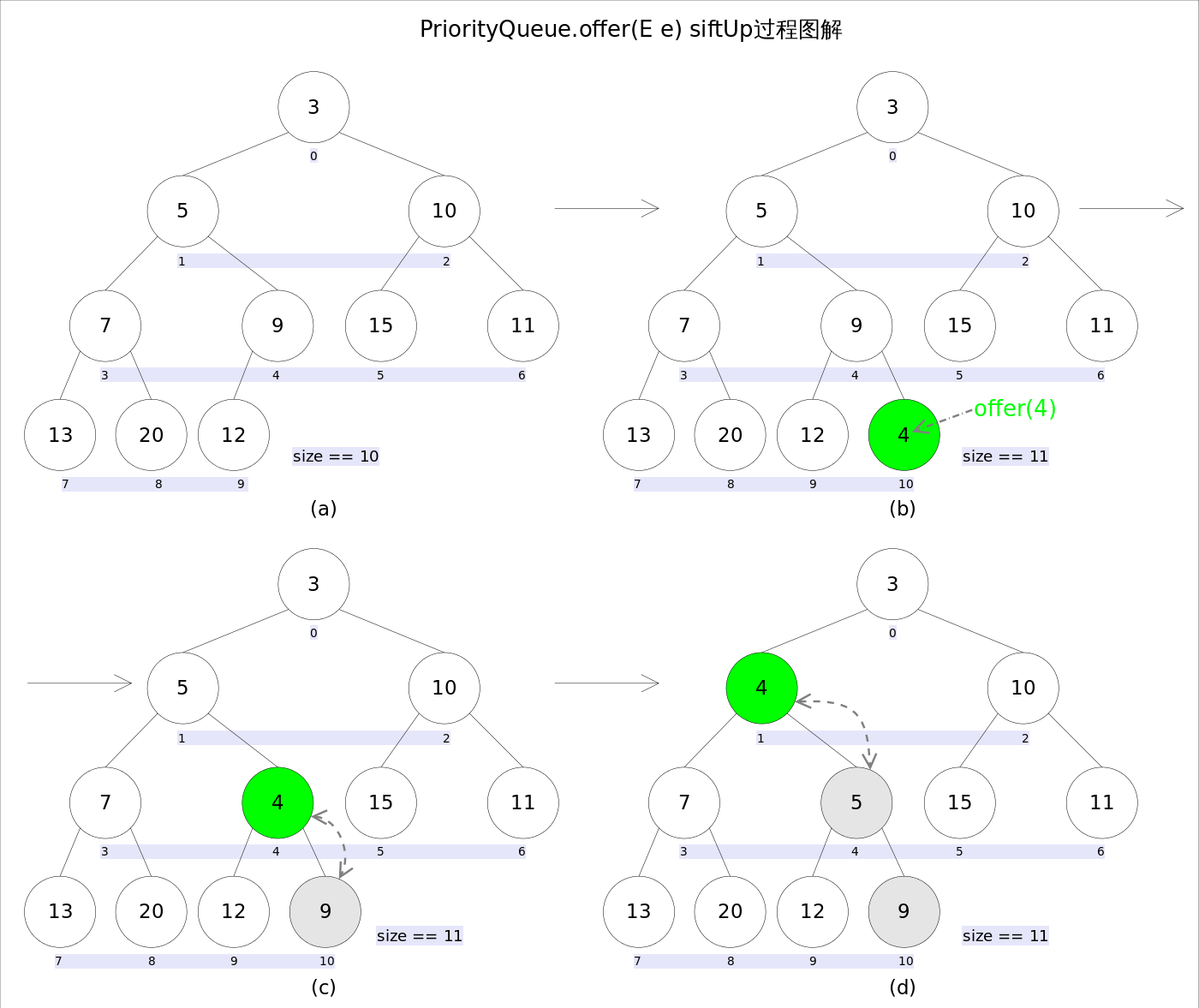
小根堆的插入

弹出（pop）

优先队列的弹出操作指将根节点移出队列，对于小根堆就是弹出队列中的最小值，对于大根堆就是弹出队列中的最大值

弹出操作的流程有点类似于插入操作的逆操作，流程大致如下：

  1. 将根节点与堆的最后一个节点调换位置
  2. 将堆的最后一个节点移出，即对堆的数组调用 pop 方法
  3. 从根节点出发，将其与子节点作比较，若不满足大小关系则与子节点交换
  4. 重复比较直至满足大小关系

这样的流程也被成为 下沉(poll) 操作，小根堆的弹出流程大致如下图所示：

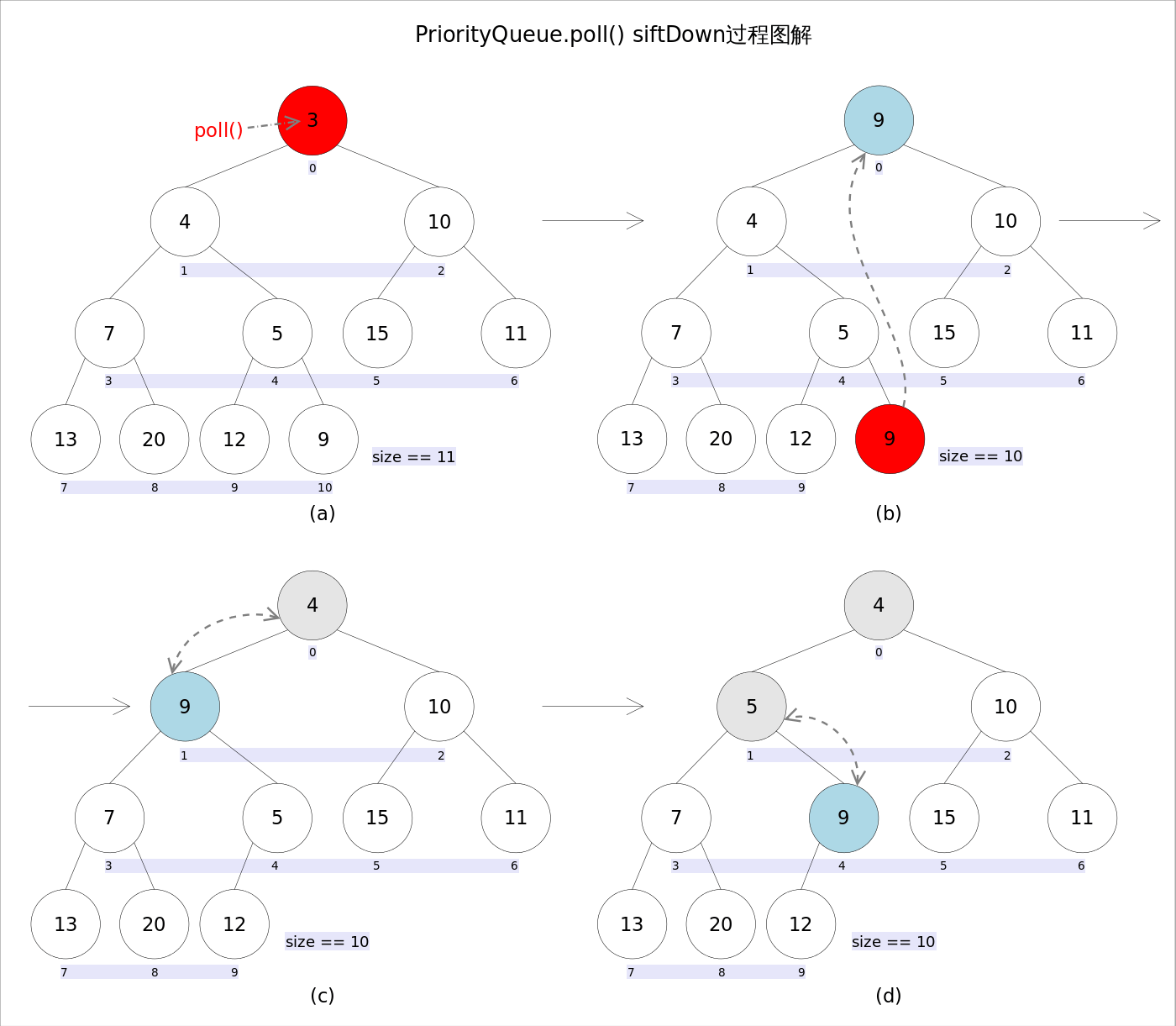
小根堆的弹出

代码实现

优先队列的有许多实例方法，例如 top、empty 等，以下是 TypeScript 的一个简单实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82

export class PriorityQueue<T> {
  private heap: T[]
  /**
   * 用于比较父节点和子节点的关系，返回值为 true 代表不满足要求需要交换节点
   * 反之说明满足要求，不需要交换节点
   * 例如 `parent < node` 时交换节点，说明大的节点在上，即大根堆
   * @example
   * (parent: number, node: number) => parent < node)
   */
  private compareFn: (parent: T, child: T) => boolean
  constructor(compareFn: (parent: T, child: T) => boolean) {
    this.heap = []
    this.compareFn = compareFn
  }
  // 获取队列长度
  public size(): number {
    return this.heap.length
  }
  // 判断队列是否为空
  public isEmpty(): boolean {
    return this.heap.length === 0
  }
  // 获取队头元素
  public top(): T | undefined {
    return this.heap[0]
  }
  // 入队操作
  public push(item: T): void {
    // heap.length 就是对应下一个节点的下标
    let i = this.heap.length
    let parentIndex: number
    while (i !== 0) {
      // 奇数，是左节点
      if (i & 1) parentIndex = (i - 1) / 2
      // 偶数，是右节点
      else parentIndex = (i - 2) / 2
      // 判断与根节点的关系
      if (this.compareFn(this.heap[parentIndex], item)) {
        this.heap[i] = this.heap[parentIndex]
        i = parentIndex
      } else break
    }
    this.heap[i] = item
  }
  // 出队操作
  public pop(): T | undefined {
    // 队列长度不超过 1 时，直接返回队头
    if (this.heap.length <= 1) return this.heap.pop()
    const res = this.heap[0]
    this.heap[0] = this.heap.pop()!
    // 从队头出发，调整队列
    let i = 0
    while (2 * i + 1 < this.heap.length || 2 * i + 2 < this.heap.length) {
      // 左节点存在
      if (
        2 * i + 1 < this.heap.length &&
        this.compareFn(this.heap[i], this.heap[2 * i + 1])
      ) {
        // 不满足就交换
        let temp = this.heap[i]
        this.heap[i] = this.heap[2 * i + 1]
        this.heap[2 * i + 1] = temp
        i = 2 * i + 1
        continue
      }
      // 右节点存在
      if (
        2 * i + 2 < this.heap.length &&
        this.compareFn(this.heap[i], this.heap[2 * i + 2])
      ) {
        // 不满足就交换
        let temp = this.heap[i]
        this.heap[i] = this.heap[2 * i + 2]
        this.heap[2 * i + 2] = temp
        i = 2 * i + 2
        continue
      }
      break
    }
    return res
  }
}

使用优先队列，我们再来解决一下开头提到的问题

获取中位数

我们这里使用优先队列 left 来记录数组的左半部分，使用 right 来记录数组的右半部分，我们需要维护这两个优先队列，使得 left 的长度要么与 right 相同，要么比它多 1

这里实际上对应着两者总长度为奇数和偶数的两种情况，总长为奇数时，中位数就是 left 的队头，偶数时则是两者队头的平均数，以下是详细的代码实现

代码实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

class MedianFinder {
  // 用 left 保存较小的一半
  public left: PriorityQueue<number>
  // 用 right 保存较大的一半
  public right: PriorityQueue<number>
  /**
   * 规定 left 的长度要么与 right 相同，要么比它多 1
   * 这样，当总长度为奇数时，中位数就是 left 的堆顶
   * 当总长度为偶数时，中位数就是 left 堆顶和 right 堆顶的平均值
   */

  constructor() {
    // 左边是大根堆 maxHeap
    this.left = new PriorityQueue<number>((parent, node) => parent < node)
    // 右边是小根堆 minHeap
    this.right = new PriorityQueue<number>((parent, node) => parent > node)
  }

  addNum(num: number): void {
    /**
     * 分情况，如果 num < left.top() 说明这个数小于中位数，应当位于左边
     * 那么就需要把当前的中位数加入 right 队列中，然后再把 num 入队 left
     */
    if (num < this.left.top()!) {
      this.right.push(this.left.pop()!)
      this.left.push(num)
    } // 反之说明这个数大于中位数，应当位于右边
    else {
      this.right.push(num)
      // 此时需要检查 right 队列的长度
      // 如果 right 超越了 left 的长度，则需要重新平衡
      if (this.right.size() > this.left.size()) {
        this.left.push(this.right.pop()!)
      }
    }
  }

  findMedian(): number {
    if (this.left.size() > this.right.size()) {
      // left 的长度长于 right 的长度，中位数就是 left 的队头
      return this.left.top() ?? 0
    }
    return ((this.left.top() ?? 0) + (this.right.top() ?? 0)) / 2
  }
}
© 2020 - 2023 一只废柴的小窝
Built with Hugo
主题 Stack 由 Jimmy 设计